동작과정만 알면 세상에서 제일 쉬운 퀵소트
void quicksort(int* a, int left, int right) {
if (right > left) {
// divide
int pivot = partition(a, left, right);
// conquer
quicksort(a, left, pivot - 1 );
quicksort(a, pivot + 1, right);
}
}
> 과정
Subarray A (코드에서 int* a) 를
1. Divide - partition(a, left, right);
두 개의 subarray a[left, pivot] 과 a[pivot+ 1, right] 로 나눈다
partition 한 결과 배열을 두개로 나누는 기준점이 되는 pivot의 값을 return한다
2. Conquer - quicksort(a, left, pivot - 1 ); , quicksort(a, pivot + 1, right);
두 배열을 Quicksort 재귀호출을 이용해 정렬한다.
3. Combine - 합치기
partition 함수에서 이미 pivot값은 자기 자리를 찾아가 정렬이 되기 때문에 subarray 를 합치는 작업은 필요하지 않는다
> partition() 동작 과정
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
/* psudo code */
partition(a, p, r){
// PARTITION always selects the last element A[r] in the subarray A[p .. r] as the pivot
x <- a[r] // partion 함수는 subarray A[p .. r]의 마지막요소인 A[r]를 pivot으로 선택합니다
i <- p – 1
for(j<- p to r-1)
do if a[j] <= x
then i<= i+1
exchange a[i] <-> a[j]
exchange a[i+1] <-> a[r]
return i + 1;
}
|
cs |
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
/* C */
int partition(int* a, int left, int right) {
int pivot = a[right];
int i = left – 1;
for (int j = left; j < right; j++) {
if a[j] <= pivot {
i++;
swap(a[i], a[j]);
}
}
swap(a[i + 1], a[right]);
return i + 1;
}
|
cs |
Loop invariant:
1. All entries in A[p .. i ] £ pivot
2. All entries in A[i+1 .. j-1] > pivot
3. A[r] = pivot
인덱스 i 는 pivot보다 작거나 같은 수들의 마지막 인덱스.
for 반복문으로 j를 right 이전 값 ( = n - 1 ) 까지 검사해 ★pivot 보다 A[j]가 작다면 A[j]를 i + 1 위치에 이동★ 시킨다.
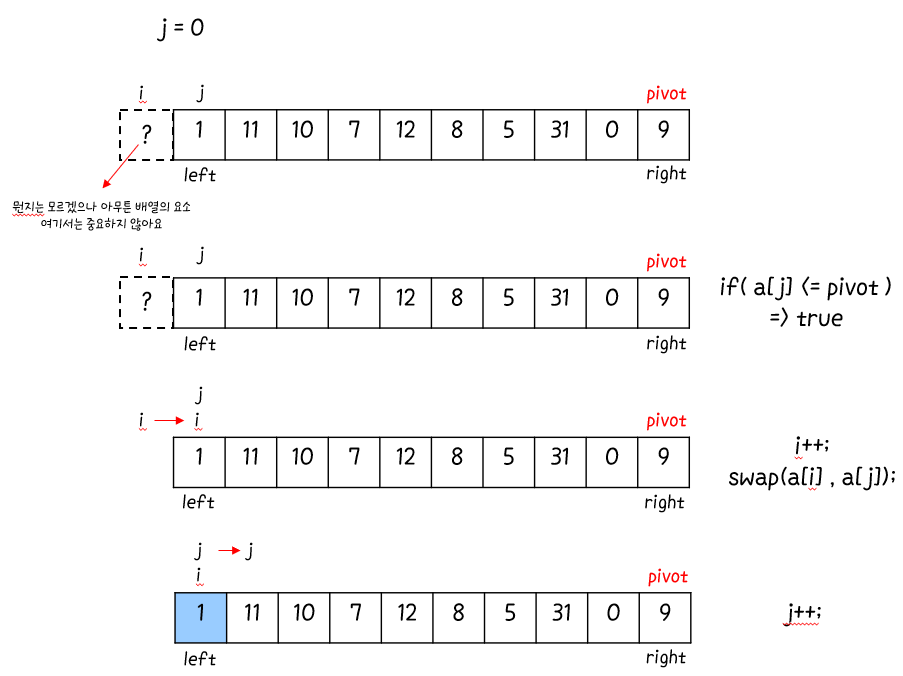
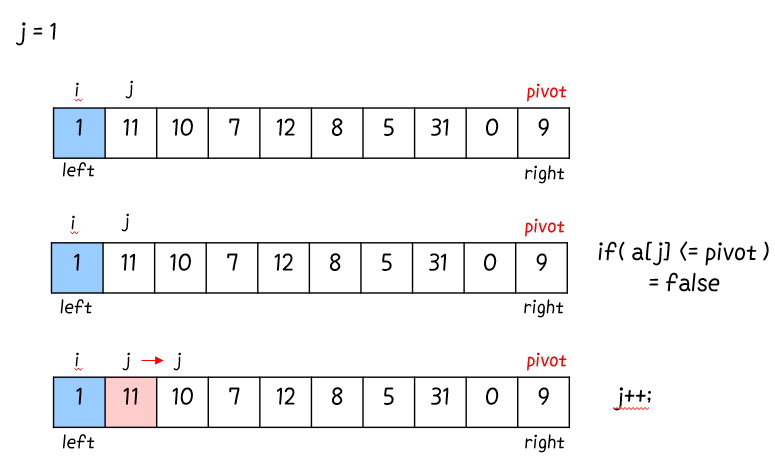
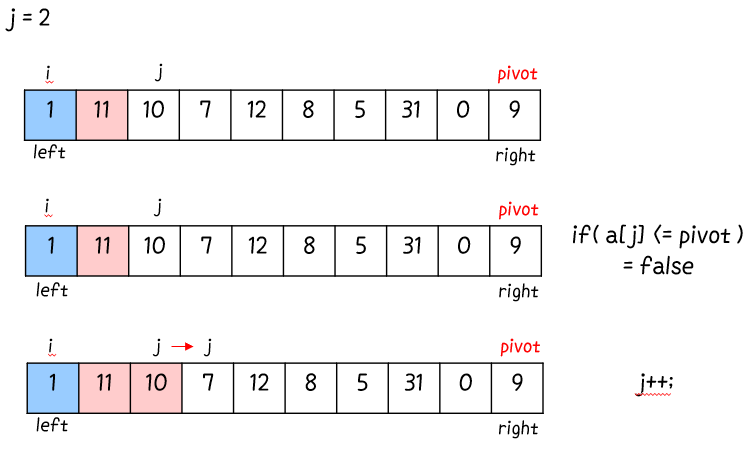
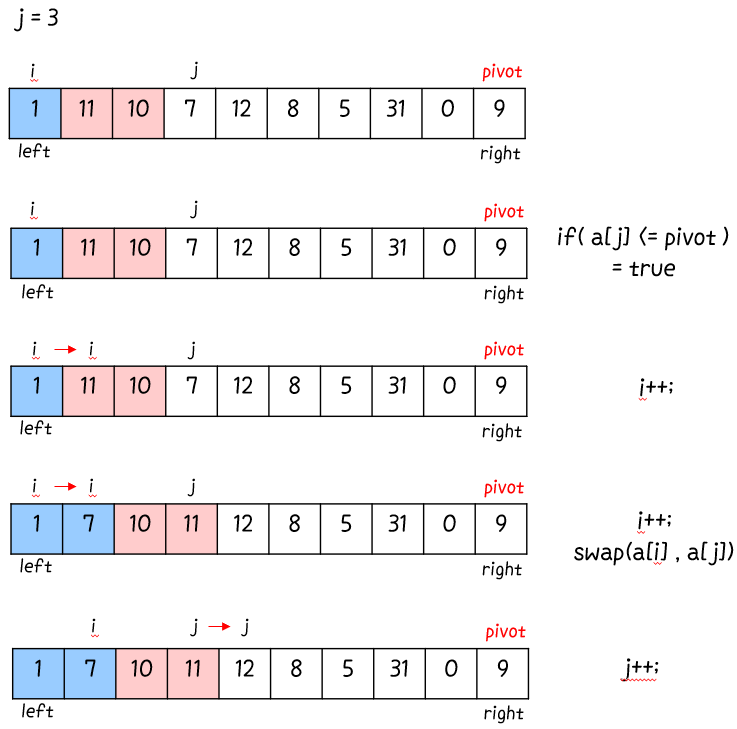
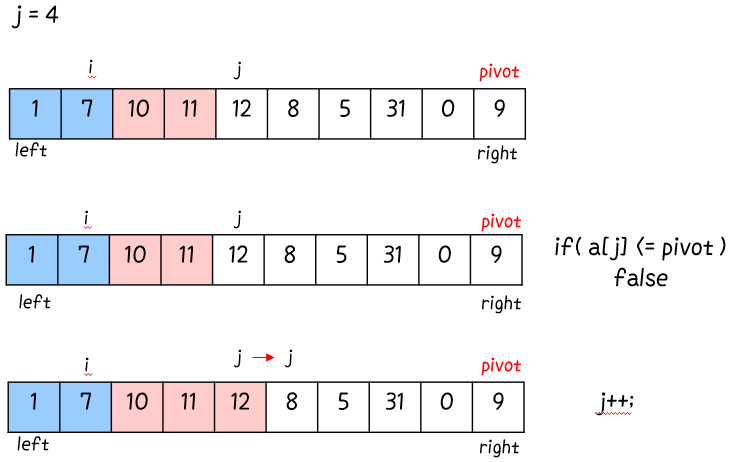
루프 for (int j = left; j < right; j++) 를 돌면서 확실한 건
A[left ... i ] <= pivot, pivot < A[i+1 ... j-1 ] 라는 점.
그리고 A[j … right - 1] 은 아직 확인되지 않은 값. A[j] 는 if (a[j] <= pivot) 을 거쳐 확인해봐야 pivot보다 작은 지 큰 지 알 수 있다.

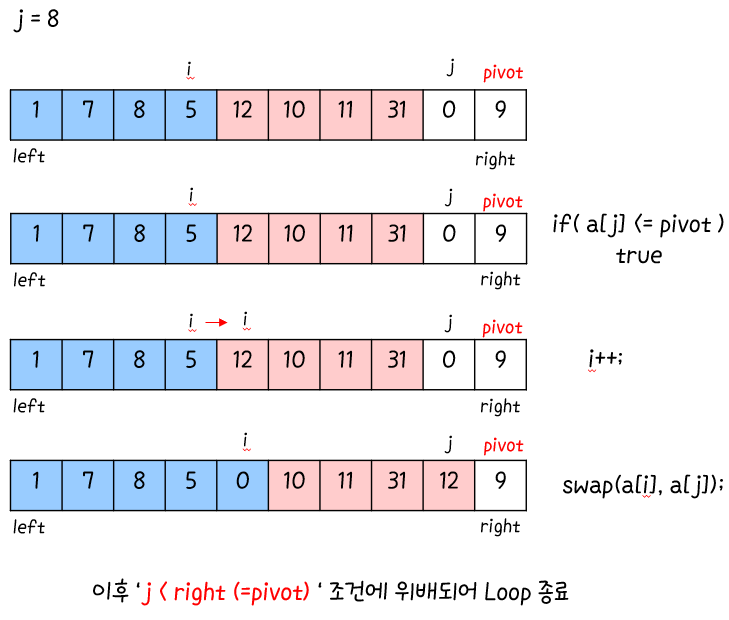
반복문은 j가 right가 될 때 종료. 종료 이후에 A는 세가지의 경우로 나뉜다.
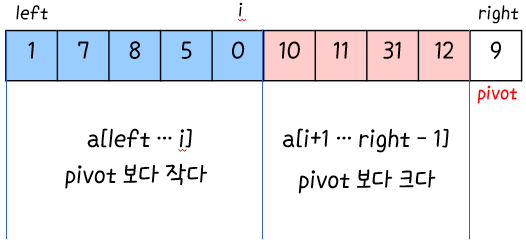
1. A[left… i] <= pivot
2. pivot < A[i+1 … right - 1]
3. A[right] = pivot
마지막 라인 swap(a[i+1], a[j]); 은 pivot 값을 두 subarrays의 사이로 옮기는 것.

이렇게 되면 pivot을 기준으로 pivot의 왼쪽은 작은놈, pivot의 오른쪽은 큰놈이 오게 된다.
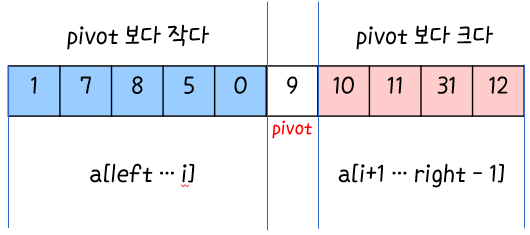
pivot: 앞과 뒤의 요소들의 순서는 난 모르겠고 내앞에 작은놈 내뒤에는 큰놈들만 있으니 내 위치는 완벽
Time for partitioning (시간복잡도)
: pivot에 대해서 나머지 n-1 개의 각 원소들과 한번씩 비교를 하기 때문에 O(n-1) => O(n)
void quicksort(int* a, int left, int right) {
if (right > left) {
int pivot = partition(a, left, right);
quicksort(a, left, pivot - 1 );
quicksort(a, pivot + 1, right);
}
}
<14> performance of Quicksort
quick sort의 running time 은 subarray 의 patitioning 에 아주아주 영향을 받음
<15> Worst Case = Array 분할 시 불균등하게
최악의 경우는 정렬하려는 리스트가 이미 한쪽으로 (오름차순이든 내림차순이든) 정렬 되어있는 상태
오름차순의 경우: ( 왼쪽 partition의 원소 0 오른쪽 partition의 원소 n – 1 (왼쪽 리스트가 텅 빈 상태))
내림차순의 경우: ( 왼쪽 partition의 원소 n-1 오른쪽 partition의 원소 0 (오른쪽 리스트가 텅 빈 상태))
> 이럴 때 sub-problem 이 하나만 생긴다
따라서 T(n) = T(n – 1) + n – 1 (n = 1) 이고
T(n) = T(n – 1) + n – 1 = T(n-1) + O(n) (n > 1)
T(n) = (n – 1) + (n – 2) + ( n - 3 ) + …. + 1 = n(n-1)/2 가 되어 시간복잡도는 세타(n^2) 이 된다
<16> Best case = Array 분할 시 양쪽으로 균등하게 분할되는 경우
만약 pivot 값이 아주 이상적으로 선정되어 매 과정마다 거의 균등한 크기로 분할이 된다면 mergesort 만큼 빠르다!
T(n) = 0 (n = 1 일 경우)
T(n) = T(n/2) + T(n/2) + n – 1 = T(n/2) + T(n/2) + O(n) (n > 1) 일 경우
if the subarrays are balanced, then quicksort can run as fast as mergesort
=> 시간복잡도는 세타(nlogn) 이 된다
<17 - 18> 두개로 나뉘긴 했는데 그 중에서도 ‘두개로 나뉘긴 했는데 한쪽에 극단적으로 치우친 케이스’
T(n) <= T(9n/10) + T(n/10) + O(n) 임에도 불구하고 O(nlgn) 이 나온다는 사실
은 recursive tree 를 그려서 해결해보자



